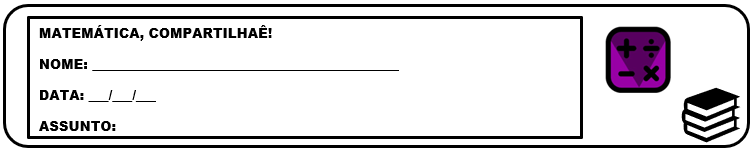
Ângulos

· Definição:

Abertura entre duas semirretas ou segmentos de retas que compartilham o mesmo ponto inicial.

Eles são medidos em graus

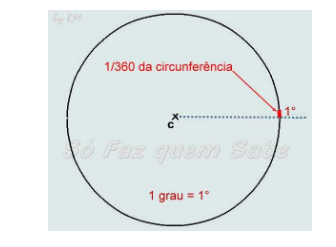
Grau(xº):

1 grau= 1º

1º= 1/360 da circunferência

OBS: uma circunferência tem ao todo 360º

· Tipos de ângulos

Para classificar um ângulo levamos em consideração a sua medida.

1. Agudo: são os ângulos que medem menos de 90º

Exemplo:

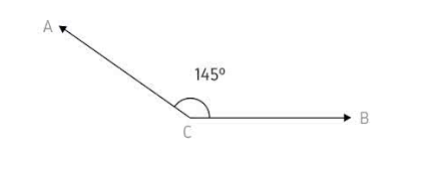
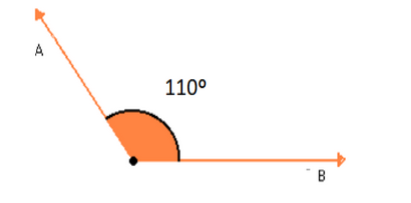
2. Obtuso: são os ângulos que medem mais de 90º

Exemplo:

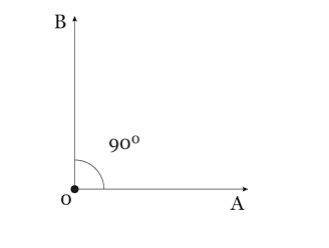
3. Reto: são os ângulos que medem exatamente 90º

Exemplo:

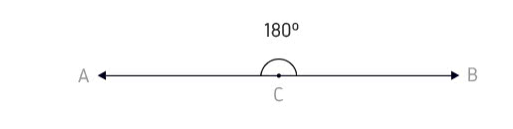
4. Raso: são os ângulos que medem 180º

Exemplo:

· Relação entre ângulos

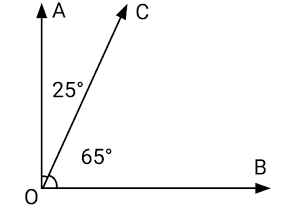
1. Ângulos complementares:

São dois ou mais ângulos que somados resultam em 90º

Exemplo:

Nesse caso, 25º+65º= 90º então eles são complementares um do outro

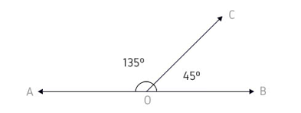
2. Ângulos suplementares:

São dois ou mais ângulos que somados resultam em 180º

Exemplo:

Nesse caso, 135º+ 45º= 180º então eles são suplementares um do outro

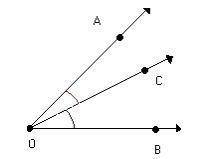
3. Ângulos adjacentes

Dois ângulos são adjacentes quando são consecutivos e não possuem pontos internos comuns

Exemplo:

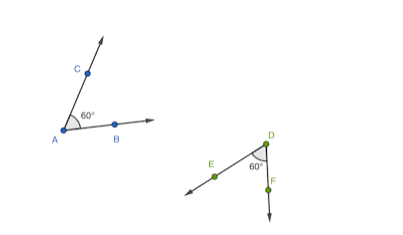
4. Ângulos congruentes

São aqueles ângulos que tem a mesma medida

Exemplo:

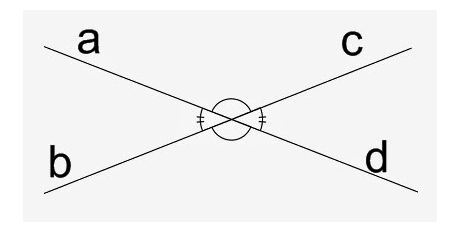
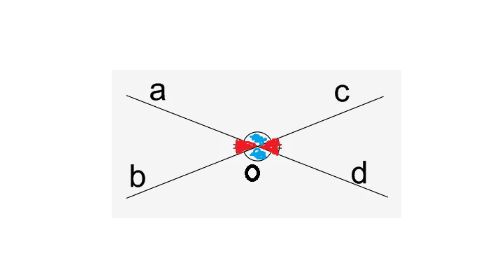
5. Ângulos opostos pelo vértice (OPV)

São aqueles cujos lados se opõem aos lados de outro ângulo.

Exemplo:

Nesse caso, o ângulo bôa e o ângulo dôc são iguais pois são opostos pelo vértice, assim como os ângulos aôc e bôd

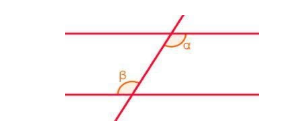
6. Ângulos alternos internos

São os ângulos que se encontram no interior das retas paralelas transpassadas por uma transversal.

Desta forma, o ângulo α (alfa) e β (beta) são iguais

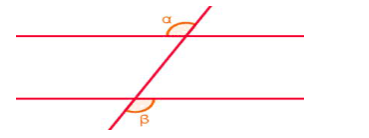
7. Ângulos alternos externos

são os ângulos que se encontram do lado externo das paralelas e, também, são aqueles que se encontram em lados opostos em relação ao outro.

Exemplo:

Assim como o ângulo alternos internos, α (alfa) e β (beta) serão iguais

EXERCÍCIOS

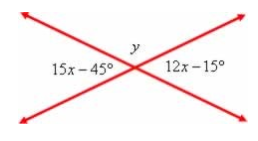
1- Determine os valores de x e y nas figuras a seguir:

2- (SAP SP). Um arquiteto, em um de seus projetos, fez algumas medições e dentre elas mediu dois ângulos complementares. Um desses ângulos mediu 65º e o outro,

a) 115º.

b) 90º.

c) 180º.

d) 25º.

e) 60º.

3- (Prefeitura de Taquarituba – SP – Instituto Excelência). Analise a figura abaixo, classifique o ângulo indicado e assinale a alternativa CORRETA:

a) Ângulo obtuso.

b) Ângulo agudo

c) Ângulo reto.

d) Nenhuma das alternativas.

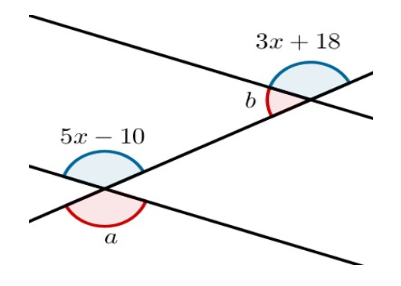
4- Dadas as retas paralelas cortadas por uma transversal a seguir, calcule a + b.

a) 14°

b) 60°

c) 120°

d) 180°

e) 200°

RESOLUÇÕES

1- Os ângulos 15x – 45 e 12x – 15 são opostos pelo vértice, portanto são iguais.

15x – 45 = 12x – 15 15x – 12x = 45 – 15 3x = 30 x = 10º

Os ângulos 15x – 45º e y são suplementares, isto é, a soma entre eles resulta em 180º.

15x – 45 + y = 180 15 * 10 – 45 + y = 180 150 – 45 + y = 180 105 + y = 180 y = 180 – 105 y = 75º

2- B)

Dois ângulos são ditos complementares quando a soma da medida de ambos é igual a 90º.

Seja x a medida do ângulo desconhecido:

x + 65 = 90

3- A)

Um ângulo é chamado de obtuso sempre que a sua medida for maior que 90º e menor que 180º.

4- D)

Observe que a é oposto pelo vértice a 5x – 10 e é alterno externo a 3x + 18

Dessa forma, podemos concluir que 5x – 10 é alterno externo a 3x + 18.

Assim, podemos escrever:

5x – 10 = 3x + 18

5x – 3x = 18 + 10

2x = 28

x = 28 2

x = 14

Cada ângulo azul mede:

5x – 10 = 5·14 – 10 = 70 – 10 = 60°

Como a é oposto pelo vértice a 60°, a = 60°.

Como b é adjacente a 60°, b é suplementar a 60°, logo, b = 120°.

A soma a + b é:

a + b = 60 + 120 = 180°